蒙特·卡罗方法(Monte Carlo method),也称统计模拟方法,是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明,而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。与它对应的是确定性算法。蒙特·卡罗方法在金融工程学,宏观经济学,计算物理学(如粒子输运计算、量子热力学计算、空气动力学计算)等领域应用广泛。
蒙特卡罗方法最典型的应用是求圆周率π,如下图,在坐标系中,有一个以(0,0)为圆点,半径为1的圆,接下来画一个边长为2的正方形,做到把圆内切在正方形上,如图:
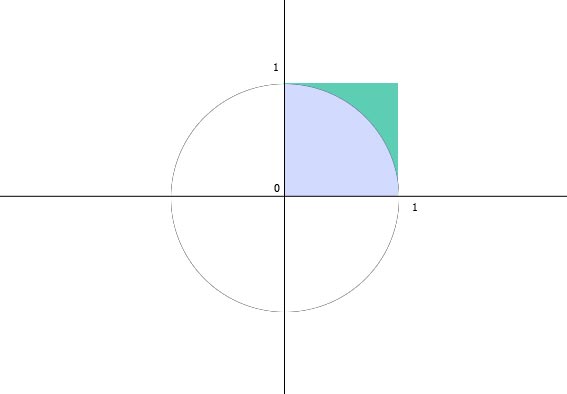
第一象限中正方形的面积为1×1=1,1/4圆的面积为πx1x1/4=π/4,我们可以领用统计学中的方法,从(0,0)到(1,1)取N多个随机点,最终在圆内的点的个数与随机点总数的比值应该是它们面积的比值,即π/4,随机点越多,π的精确度越高,那么求π的程序可以如下:
#!/usr/bin/env python
import random
import math
def getpi(count):
i = 0
k = 0.0
while i < count:
x = random.random()
y = random.random()
if math.sqrt(x*x + y*y) < 1:
k+=1
i+=1
return k/(count*0.25)
利用上面的函数,以不同的采样点个数来计算圆周率,分别得出以下结果:
| 采样个数 | 结果 |
| 2000 | 3.118 |
| 20000 | 3.1534 |
| 200000 | 3.13914 |
| 2000000 | 3.14263 |
| 2000000 | 3.141697 |
| 200000000 | 3.141618586 |
可以看出,采样点越多,圆周率越接近实际值,正好印证了统计学中“样本数量越多,统计结果越精确”的思想。
第二个例子是求抛物线的面积,如图,求函数y=x^2与x轴,x=1组成的面积
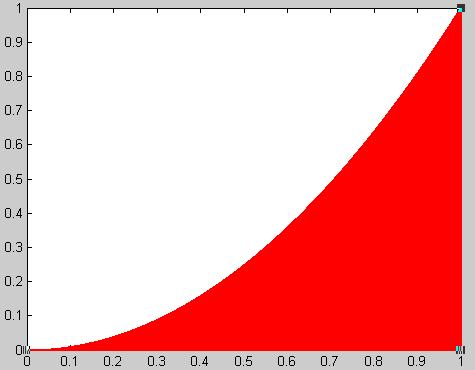
传统的方法是用微积分的方式:
![]()
用统计学的方法进行计算
#!/usr/bin/env python
import random
def getarea(count):
i = 0
k = 0.0
while i < count:
x = random.random()
y = random.random()
if y < x*x:
k+=1
i+=1
return k/count
不同的取样数最终得出如下结果:
| 采样个数 | 结果 |
| 2000 | 0.3395 |
| 20000 | 0.33535 |
| 200000 | 0.333105 |
| 2000000 | 0.3334275 |
| 2000000 | 0.333366 |
| 200000000 | 0.333341816 |
随机数
上述蒙特卡洛方法的关键在生成大量的随机数并对其范围进行统计,那么对随机数生成就有一个必备的条件“分布均匀”,我们的生成随机数的办法均匀吗,这里我用以下程序获取固定的随机数,并对其分布进行观察
#!/usr/bin/env python
# -*- coding:utf-8 -*-
import matplotlib.pyplot as plt
import random
def showpic(count):
i = 0
while i < count:
x = random.random()
y = random.random()
plt.scatter(x,y,s=5,alpha=0.6)
i+=1
plt.show()
得出随机点的分布图
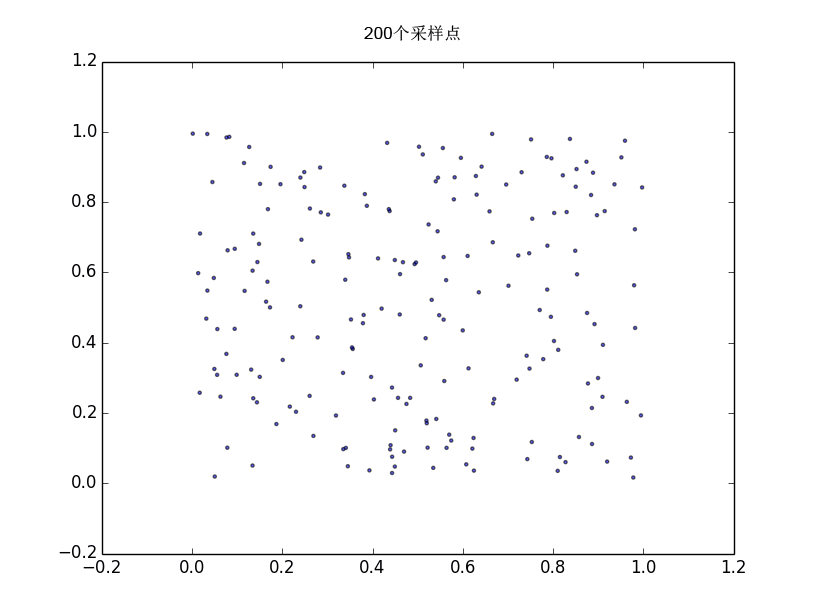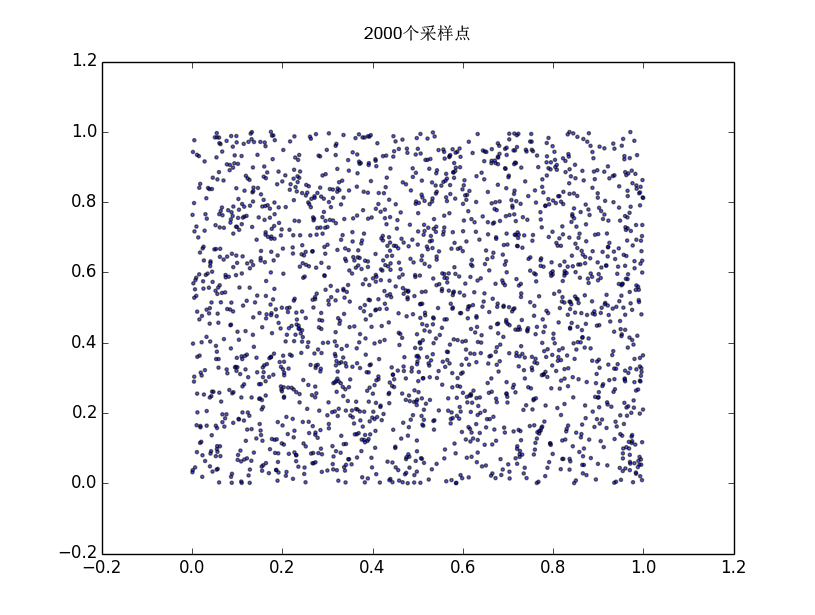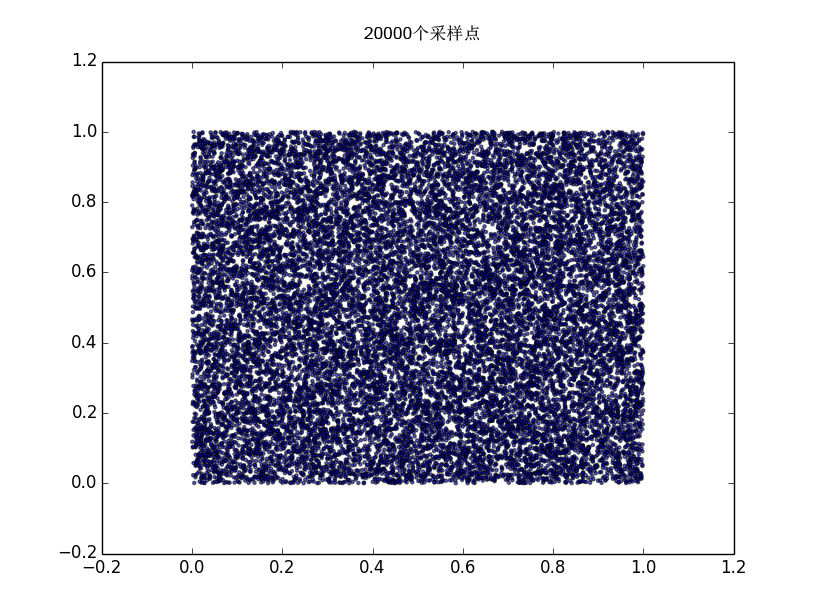
可以看出随机点分布遵循了均匀分布的原则。我们知道,随机数可以分为真随机数和伪随机数,真随机数是那些完全无法预测的随机数,一般通过真随机数生成器来生成真随机数,真随机数生成器利用完全无法预测的事件如键盘的敲击时间,外接噪音的大小,粒子的衰变发生时间等来生成随机数,linux中/dev/random就是一个真随机数生成器,其生成效率较低,另外一个/dev/urandom则是伪随机数生成器,它利用已经存在的熵池中的数据来生成随机数。
在实际需求中,如果对安全性要求高,则使用真随机数,如果对随机数的生成效率要求高,则更多使用伪随机数。伪随机数由程序生成,一个好的随机数算法应该有以下一个特征:
1, 相同序列的概率非常低
2, 符合统计学的平均性,比如所有数字出现概率应该相同,卡方检验应该能通过,超长游程长度概略应该非常小,自相关应该只有一个尖峰,任何长度的同一数字之后别的数字出现概率应该仍然是相等的等等
3, 不应该能够从一段序列猜测出随机数发生器的工作状态或者下一个随机数
4, 不应该从随机数发生器的状态能猜测出随机数发生器以前的工作状态
目前,随机数算法主要有取中法,同余法,移位法和梅森旋转算法等。
评论列表: